Table of contents

• Bubble sort
• Searching for the maximum value
• Selection sort
• Insertion sort
• Quicksort
• sort() - the <algorithm> library

Bubble sort

Bubble sort is a simple sorting algorithm that repeatedly steps through the input list element by element, comparing the current one with the one after it, swapping their values if needed (the larger elements "bubble up" to the top of the list). These swaps through the list are repeated until they don't have to be performed, meaning the list has become fully sorted.

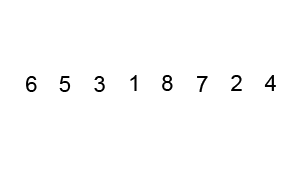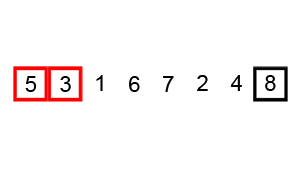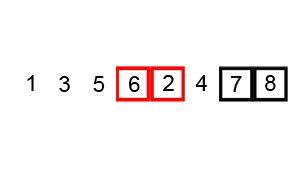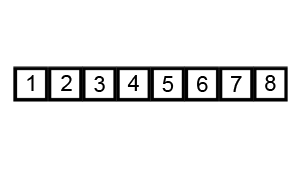
const int x = 5;
int a[x];    

for (int i = 0; i < x; i++) {
    cout << "Enter " << i + 1 << " number: ";
    cin >> a[i];
}

int t;

for (int i = 0; i < x - 1; i++) { // "x - 1" because it doesn't have to check the last number
    for (int j = 0; j < x - 1; j++) { // "x - 1" so that the "j + 1" later won't exceed the array's last index
        if (a[j] > a[j + 1]) {
            t = a[j];
            a[j] = a[j + 1];
            a[j + 1] = t;
        }
    }
}    

for (int i = 0; i < x; i++) {
    cout << i + 1 << ". = " << a[i] << endl;
}
                                    

Searching for the maximum value

We can search for the maximum value in an array in three ways. Firstly, we can use a normal array and a loop. Secondly, we can apply a similar method with vectors so that we don't have to know how many numers there are. At last, we can use a pre-made method from the <algorithm> library.

const int x = 5;
int array[x] = {20, 2, -4, 150, 40};

int maxV = array[0];
for (int i = 0; i < x; i++) {
    if (maxV < array[i])
        maxV = array[i];
}
cout << maxV << endl;
                                    

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int findMax(vector<int> numbers) {
    int maxV = numbers[0];
    for (auto n : numbers) {
        if (maxV < n)
            maxV = n;
    }
    return maxV;
}

int main() {
    int a = 4, b = 2, c = 50;
    cout << findMax({a, b, 40, c, -20}) << endl;
    
    vector<int> tempVector = {a, b, c};
    
    cout << *max_element(array, array + x) << endl; // "*max_element" is from the <algorithm> library
    cout << *max_element(tempVector.begin(), tempVector.end()) << endl;
    
    return 0;
}
                                    

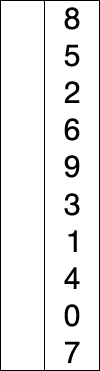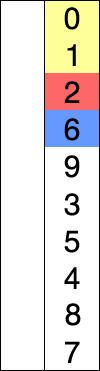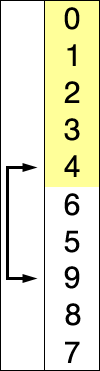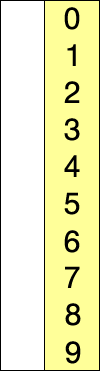
Selection sort

Selection sort is an in-place comparison sorting algorithm. It is inefficient on large arrays. Selection sort is noted for its simplicity and has performance advantages over more complicated algorithms in certain situations, particularly where auxiliary memory is limited.

const int x = 4;
int a[x];

for (int i = 0; i < x; i++) {
    cout << "Enter " << i + 1 << " number: ";
    cin >> a[i];
}

int k, t;

for (int i = 0; i < x - 1; i++) {
    k = i;
    for (int j = i + 1; j < x; j++) {
        if (a[j] < a[k])
            k = j;
    }
    t = a[i];
    a[i] = a[k];
    a[k] = t;
}

for (int i = 0; i < x; i++) {
    cout << i + 1 << ". = " << a[i] << endl;
}
                                    

Insertion sort

Insertion sort is a simple sorting algorithm that builds the final sorted array one item at a time by comparisons. It is much less efficient on large lists than more advanced algorithms such as quicksort. However, it is more efficient than selection sort and bubble sort.

const int x = 4;
int a[x];

for (int i = 0; i < x; i++) {
    cout << "Enter " << i + 1 << " number: ";
    cin >> a[i];
}

int y, i, j;

for (j = x - 2; j >= 0; j--) {
    y = a[j];
    i = j + 1;
    while ((i < x) && (y > a[i])) {
        a[i - 1] = a[i];
        i++;
    }
    a[i - 1] = y;
}

for (int i = 0; i < x; i++) {
    cout << i + 1 << ". = " << a[i] << endl;
}
                                    

Quicksort

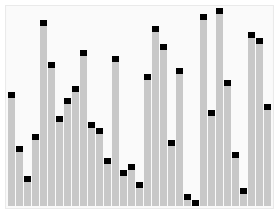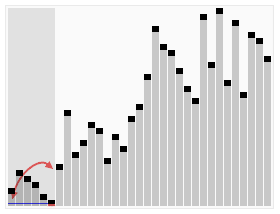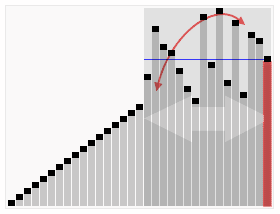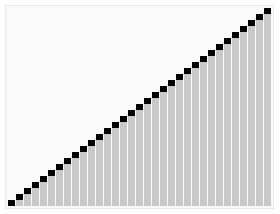
Quicksort is an efficient, general-purpose sorting algorithm. It is a divide-and-conquer algorithm. It works by selecting a "pivot" element from the array and partitioning the other elements into two sub-arrays according to whether they are lesser or greater than the pivot. The sub-arrays are then sorted recursively. It can be used in-place, requiring small additional amounts of memory to perform the sorting.

_{The horizontal lines are pivot values.}

#include <iostream>
using namespace std;

const int x = 5;
int a[x] = {5, 60, 10, 40, 3};

void sort(int left, int right) {
    int i, j, t, pivot;
    
    i = (left + right) / 2;
    pivot = a[i];
    a[i] = a[right];
    
    for (j = i = left; i < right; i++) { // "i" gets a value from "left" and "j" gets a value from "i"
        if (a[i] < pivot) {
            t = a[i];
            a[i] = a[j];
            a[j] = t;
            j++;
        }
    }
    a[right] = a[j];
    a[j] = pivot;
    if (left < j - 1)
        sort(left, j - 1);
    if (j + 1 < right)
        sort(j + 1, right);
}

int main() {
    sort(0, x - 1);
    
    for (int i = 0; i < x; i++) {
        cout << i + 1 << ". = " << a[i] << endl;
    }
    return 0;
}
                                    

sort() - the <algorithm> library

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

bool descending(int a, int b) {
    return a > b;
}

int main() {
    // sort([array_name], [array_name] + [number_of_elements_to_sort], optional: the descending function);
    // *Ascending sort is the default option.

    // Sorting arrays
    int a[] = {9, 8, 7, 0, 8, 6, 3, 1, 7, 2};
    sort(a, a + 10, descending);
    for (int i = 0; i < 10; i++)
        cout << a[i] << endl;

    // Sorting vectors
    vector<int> b {9, 8, 7, 0, 8, 6, 3, 1, 7, 2};
    sort(b.begin(), b.end(), descending);
    for (int x : b)
        cout << x << endl;

    return 0;
}