Table of contents

• Finding prime numbers
• Generating prime numbers
• Sieve of Eratosthenes
• Euclidean algorithm

Finding prime numbers

Prime numbers are numbers that have only 2 factors: 1 and themselves.

#include <iostream>
#include <cmath>
using namespace std;

bool isPrime(int x) {
    if (x <= 1) return false;
    for (unsigned int i = 2; i <= sqrt(x); i++) { // 0 and 1 are not prime numbers
        if (!(x % i))
            return false;
    }
    return true;
}

int main() {
    int x;
    cin >> x;
    if (isPrime(x))
        cout << "This number is a prime number." << endl;
    else
        cout << "This number isn't a prime number." << endl;
    return 0;
}
                                    

Generating prime numbers

#include <iostream>
#include <cmath>
using namespace std;

bool isPrime(int x) {
    if (x <= 1) return false;
    for (unsigned int i = 2; i <= sqrt(x); i++) {
        if (!(x % i))
            return false;
    }
    return true;
}

int main() {
    int x, y;
    
    cout << "How many prime numbers should I generate: ";
    cin >> y;
    
    for (unsigned int i = 0; i < y; i++) {
        if (isPrime(x))
            cout << x << endl;
        else
            i--;
        x++;
    }
    
    return 0;
}
                                    

Sieve of Eratosthenes

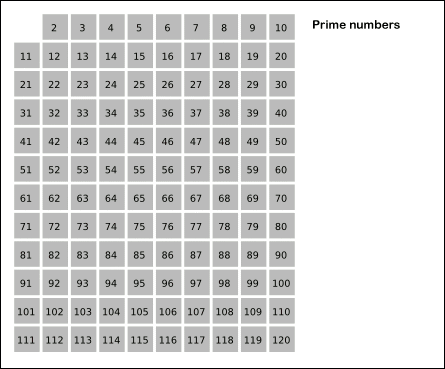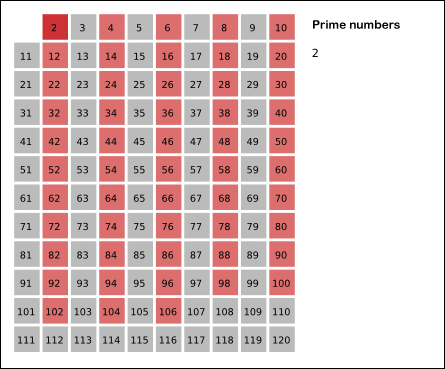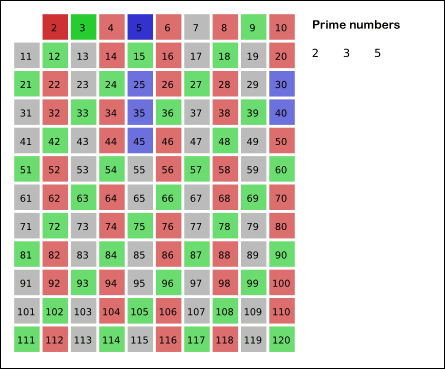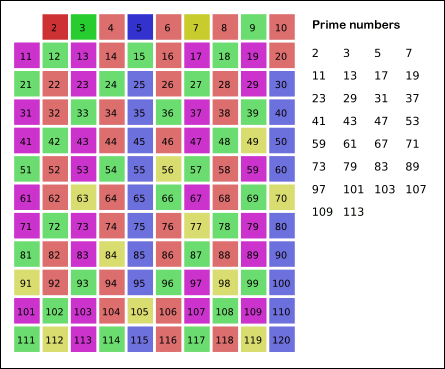
The Sieve of Eratosthenes is an efficient algorithm for finding all prime numbers up to any given limit. It does so by iteratively marking as composite (i.e., not prime) the multiples of each prime number.

unsigned int i, x, y;
cout << "Up to what number should I write prime numbers: ";
cin >> y;
bool *a = new bool[y];

for (i = 2; i <= y; i++) // setting the initial values
    a[i] = true;

i = 2;
while (i * i <= y) {
    if (a[i]) {
        x = i * i;
        while (x < y) {
            a[x] = false;
            x = x + i;
        }
    }
    i++;
}

for (i = 2; i <= y; i++) { // displaying the results
    if (a[i])
        cout << i << ", ";
}
                                    

Euclidean algorithm

We use the Euclidean algorithm to find the GCD (Greatest Common Divisor) of two numbers. It subtracts the smaller number from the bigger one as long as they differ. Finally, they are the same, and this is our GCD.

#include <iostream>
using namespace std;

int GCD(int x, int y) {
    while (x != y) {
        if (x > y)
            x = x - y;
        else
            y = y - x;
    }
    return x;
}

int GCD2(int x, int y) {
    int r;
    while (r = x % y) {
        x = y;
        y = r;
    }
    return y;
}

int main() {
    int x, y;

    cout << "Enter two numbers for which I should find the GCD: ";
    cin >> x >> y;

    cout << GCD(x, y) << endl;
    cout << GCD2(x, y) << endl;
    
    return 0;
}